Ábaco

Acerca de

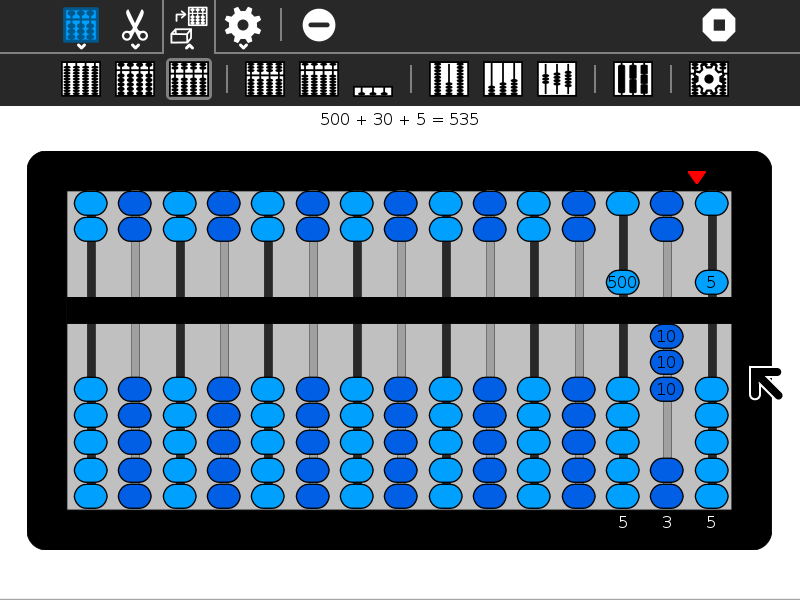
Ábaco permite al estudiante explorar diferentes representaciones de números utilizando diferentes sistemas de conteo mecánico desarrollado por los antiguos romanos y los chinos. Hay varias variantes diferentes disponibles para la exploración: el Suanpan, el ábaco chino tradicional con 2 cuentas en la parte superior y 5 cuentas por debajo; el Soroban, el ábaco japonés tradicional con 1 grano en la parte superior y 4 cuentas por debajo; el Schety, el ábaco tradicional ruso, con 10 cuentas por columna, con la excepción de una columna con sólo 4 bolas utilizadas para contar en cuartos; y el Nepohualtzintzin, un ábaco maya, con 3 cuentas en la parte superior y 4 cuentas siguientes (base 20). También hay un ábaco binario, un ábaco hexadecimal, y varios ábacos que te permite calcular con fracciones comunes: 1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10, y 1/12. Y hay una barra de herramientas de personalización que te permite diseñar tu propio ábaco. El ábaco inca (Yupana) es una actividad independiente.

El uso de Ábaco

Borrado del ábaco

Antes de iniciar una operación aritmética, es necesario “limpiar” el ábaco. Las perlas superiores deben colocarse contra la parte superior del marco y las perlas inferiores deben colocarse contra la parte inferior del marco. Esta es la posición por defecto para el ábaco al iniciar la actividad.

Ten en cuenta que algunos de los ábacos (por ejemplo, el Schety) no tienen ninguna perla superior. En tales casos, todas debe comenzar en la posición baja. También ten en cuenta que el botón Borrar en la barra de herramientas principal borrará el ábaco por ti.

Leyendo el ábaco

En cada columna, las perlas inferiores representan 1s y las perlas superiores representan 5s. (La excepción es la columna en el Schety con sólo 4 perlas. Estos valen un cuarto cada una. ) Así que por cada cuenta se eleva desde el fondo de una columna hay que agregar 1 y por cada cuenta que baja desde la parte superior de la misma columna, hay que añadir 5.

Las columnas representan por sí mismas posiciones decimales de derecha a izquierda, por ejemplo, 1s, 10s, 100s, 1000, etc.. (Hay algunas excepciones: (1) el Nepohualtzintzin utiliza de base 20, ejemplo, 1s, 20s, 400s, 8000s, etc. ; (2) en el Schety, las perlas a la derecha de la columna con sólo cuatro perlas son 0.1s, 0.01s, 0.001s y 0.001s; las perlas negras en el ábaco Caacupe tienen valores fraccionarios; y en los ábacos diseñados por el usuario las cuentas pueden tener cualquier valor entero

El valor actual se muestra siempre en el marco. Experimenta aprenderás rápidamente a leer y escribir números.

Ejemplos: En la galería a continuación, se muestran varios ejemplos sencillos. En la galería de imágenes de arriba, el número 54321 se muestra en cada uno de los diferentes ábacos.

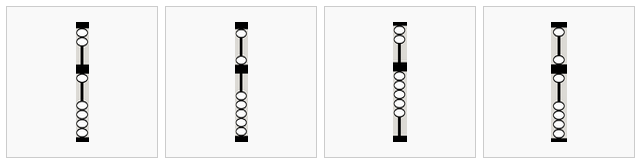
De izquierda a derecha,

• 1 perla inferior se ha levantado, que corresponde a 1 unidad

• 1 perla superior se ha bajado, correspondiente a 5 unidades

• 5 cuentas de abajo han subido, también correspondiente a 5 unidades

• 1 perla inferior está arriba y una perla de arriba está abajo, correspondiendo a 6 unidades

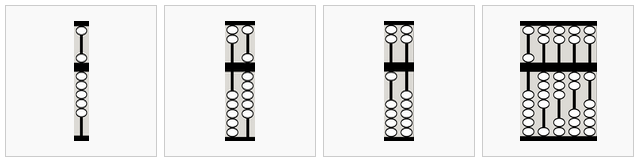
De izquierda a derecha,

• 5 cuentas de abajo estan subidas y una perla de arriba está abajo, lo que corresponde a 10 unidades (tiempo para “llevar” a la izquierda)

• Esto es equivalente a 10. . .

• . . . este 10

• 54321

Nota: La pantalla siempre asume una columna unidad fija, pero se puede anular esta elección.

Las perlas que se movieron recientemente se destacan.

Adición

Para agregar, simplemente mueve más cuentas para representar el número que está agregando. Hay dos reglas a seguir: (1) cada vez que tengas un total de 5 unidades o más en la parte inferior de una columna, cancela el 5 deslizando las cuentas de nuevo y añade un cinco a la parte superior; y (2) cada vez que tengas un total de 10 unidades o más en una columna, anula el 10 y añade una unidad a la columna inmediatamente a la izquierda. (Con el Nepohualtzintzin, se trabaja con 20 en lugar de 10. )

Ejemplo: 4 + 3 + 5 + 19 + 24 = 55

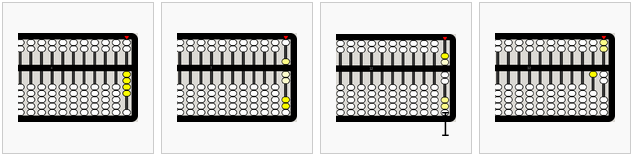
de izquierda a derecha,

• 4
• +3=7 (5–2=3)
• +5=12

• llevar 5s a la siguiente columna

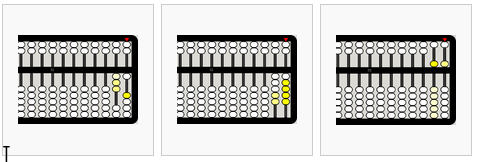
de izquierda a derecha,

• +19=31 (20-1=19)
• +24=55
• 4+3+5+19+24=55

Sustracción

La resta es la inversa de la suma. Retira cuentas que corresponden al número que estás restando. Puedes “pedir prestado” de la columna inmediatamente a la izquierda: restando una unidad y añadiendo 10 a la columna actual.

Ejemplo: 26–2–4–6–10=4

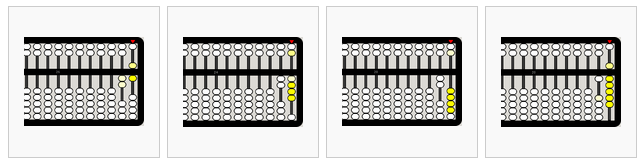
de izquierda a derecha,

• 26
• 26-2=24
• 24-4=20

• llevar 10 a la derecha

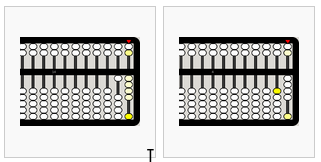
de izquierda a derecha,

• 20-6=14
• 14-10=4

Multiplicación

Hay varias estrategias para hacer la multiplicación en un ábaco. En el método utilizado en el ejemplo siguiente, el multiplicador se almacena en el extremo izquierdo del ábaco y el multiplicando está desplazado a la izquierda por el número de dígitos en el multiplicador. El indicador rojo se utiliza para ayudar a mantener un seguimiento de dónde estamos en el proceso.

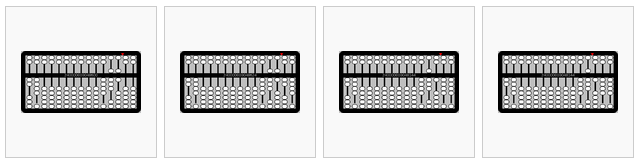
de izquierda a derecha,

• 486×24=? Comience poniendo 24 in las columnas de la izquierda y 486 a dos columnas de la derecha (ya que 24 tiene dos dígitos). Pon el indicador a la derecha del multiplicando.

• Multiplica los dígitos menos significativos (DMS) del multiplicador (4) y del multiplicando (6) y coloca los resultados (4 × 6 = 24) en las columnas de la extrema derecha.

• Multiplica el siguiente dígito en el multiplicador (2, que corresponde a 2 × 10 = 20) y el DMS del multiplicando (6) y agrega los resultados (2 × 6 = 12) a la derecha (avanza una columna a la izquierda para corresponder a la potencia del dígito en el multiplicador).

• Mueve el indicador una columna más a la izquierda.

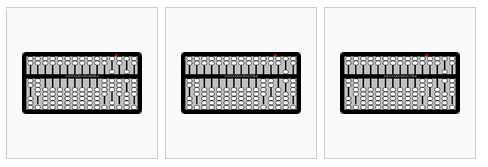
de izquierda a derecha,

• Repite para el siguiente dígito en el multiplicando (8): 4x8=32

• 2×8=16

• Mueve el indicador una columna más a la izquierda.

de izquierda a derecha,

• Repite para el siguiente dígito en el multiplicando (4): 4×4=16

• 2×4=8

• Limpia el multiplicador de la izquierda para ver el resultado: 486×24=11664

División

Una simple división (por un número de un solo dígito) es la inversa de la multiplicación. En el ejemplo siguiente, el dividendo se pone a la izquierda (dejando una columna vacante por el cociente) y el divisor a la derecha.

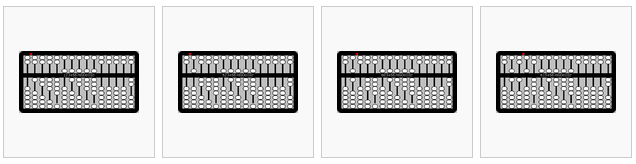
de izquierda a derecha,

• 123456789÷2=? Coloca el dividendo (123456789) a la izquierda, dejando una columna vacía. Coloca el divisor (2) a la derecha.

• Trabajando desde la izquierda a la derecha, dividir un dígito en el cociente y luego mover el indicador de una columna a la derecha. 1÷2=0.5

• 2÷2=1
• 3÷2=1.5

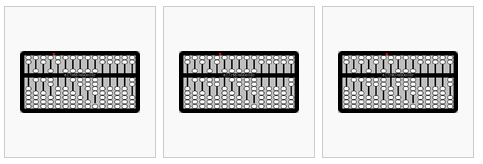
de izquierda a derecha,

• 4÷2=2
• 5÷2=2.5
• 6÷2=3

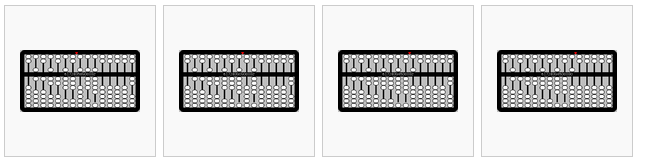
de izquierda a derecha,

• 7÷2=3.5
• 8÷2=4
• 9÷2=4.5

• El resultado es 61728394.5.

Fracciones

La ábaco con fracciones permite sumar y restar fracciones comunes: 1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10, 1/12 y, El valor fraccionario se determina por el número de perlas en negro en una varilla, ej. , Para trabajar con terceras partes, utilizar la varilla con tres cuentas, para trabajar con quintas partes, utilizar la varilla con cinco cuentas.

Las varillas con las perlas blancos son números enteros en base 10; de izquierda a derecha 100000, 10000, 1000, 100, 10, y 1.

20 + 1 + 1/2 + 1/3 + 1/6 = 22

Las barras de herramientas

De izquierda a derecha:

• boton de barra de actividad: ver más abajo

• boton de barra de edición: ver más abajo

• boton de barra de ábacos: ver más abajo

• boton de barra de personalización

• boton de limpieza: Borrado del ábaco

• boton cerrar: salir de la actividad

De izquierda a derecha:

• copiar: copia el valor del ábaco al portapapeles

• pegar: pega el valor del portapapeles en el ábaco

De izquierda a derecha:

• boton decimal: ábaco decimal

• boton Soroban: ábaco japones

• boton Saupan: ábaco chino

• boton Nepohualtzintzin: ábaco Maya

• boton hexadecimal: ábaco hexadecimal

• boton binario: ábaco binario

• boton Schety: ábaco ruso

• boton fracciones: ábaco para fracciones

• boton Caacupe: ábaco con fracciones con +/-

• boton barra: ábaco tipo Cuisenaire

• boton personalizar: tu propio ábaco

De izquierda a derecha:

• varilla: seleccionar el número de varillas

• perlas superiores: seleccionar el número de perlas en la parte superior del marco

• inferior: seleccionar el número de perlas en la parte inferior del marco

• factor: seleccionar el factor de multiplicación de las perlas superiores (ej. en el ábaco Chino, cada perla superior vale 5 veces el valor de la perla inferior en la misma varilla)

• base: seleccionar la base para determinar el valor de las perlas inferiores a traves de las varillas; es 10 en los ábacos más convencionales, pero 20 en el Maya, 16 en el hexadecimal y 2 en el ábaco binario.

• crear: debes presionar este boton para activar los parametros que has elegido

Galería de ábacos

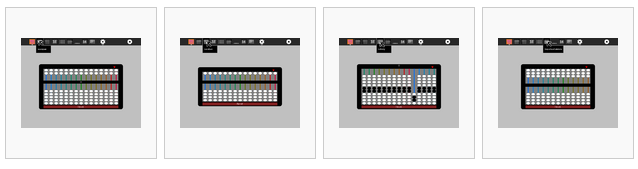
De izquierda a derecha,

• Suanpan (chino)

• Soropan (japonés)

• Schety (Rusia)

• Nepohualtzintzin (maya)

De izquierda a derecha,

• Binario (base 2)

• Hexadecimal (base 16)

• Fracciones (1/2, 1/3, 1/4,. . . )

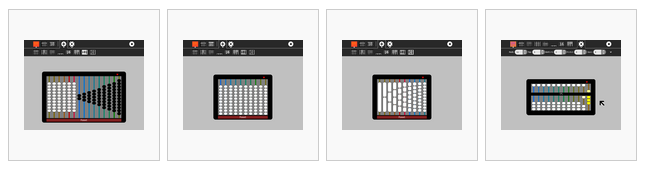
De izquierda a derecha,

• Caacupe (fracciones con +/-)

• Decimal (base 10)

• Varillas de estilo Cuisenaire (fracciones)

• Personalizado, como se muestra: octal (base 8)

Aprender con Abacus

• Algunos planes de lecciones para el uso del ábaco se encuentran aquí.

• Usando perlas o piedras, se puede hacer un ábaco. ¿Cuál es la diferencia entre el ábaco en el ordenador y un ábaco físico?

• Es posible crear un ábaco personalizado. A menudo utilizo el ejemplo de matemáticas sumerias: los sumerios contaban con los huesos (falanges) de sus dedos, por lo que la base de su sistema de conteo fue 12. Todos los 12 (y 60) que tenemos en nuestras matematicas, ej. , 12 horas, 60 segundos, etc.. tienen sus raíces en las matemáticas sumerias. Pero los sumerios nunca inventaron el ábaco. ¿Cómo crees que sería un ábaco sumerio?

Extendiendo Ábaco

• Un proyecto divertido es comparar cálculos utilizando Abacus con la actividad Calcular. ¿Qué es más rápido? ¿Qué es más preciso? ¿Qué es mejor para la estimación? ¿Qué es mejor para comparar?

• Abaco soporta ‘pegar’, así que puedes tomar valores numéricos de otros programas y pegarlos en el ábaco para ver sus representaciones; por ejemplo, a menudo pego números en el ábaco hexadecimal como una forma rápida de convertir de decimal a hexadecimal.

• Abacus también soporta ‘copiar’, para que puedas tomar una suma calculada en un ábaco y exportarlo en SimpleGraph o algunas otra-actividad de visualización de datos.

• Un modo de colaboración divertido podría ser la de tener un número seleccionado al azar y que cada partícipe independiente deba ponerlo en el ábaco de su elección. Podría haber un recuento de los granos otorgados por cada respuesta correcta.

Informar fallos

Si descubres un error en el programa o tienes una sugerencia para una mejora, por favor llena un ticket en nuestro sistema de seguimiento de bugs.

Puedes `ver los tickets abiertos aquí. <https://bugs.sugarlabs.org/query?status=accepted&status=assigned&status=new&status=reopened&component=Abacus> `_

Referencias

Página Wiki